
Software
We encountered several interesting challenges when developing the software for this competition. There is much to say about each one of them but in this section we will limit ourseleves to discussing strategy, navigation, and dealing with failure.
Strategy
Having a good strategy was an integral part of this competition. There were many different ways to score points and a limited amount of time in which to score them. After carefully examining the rules we decided that the following flowchart represented the optimal strategy for our robot.
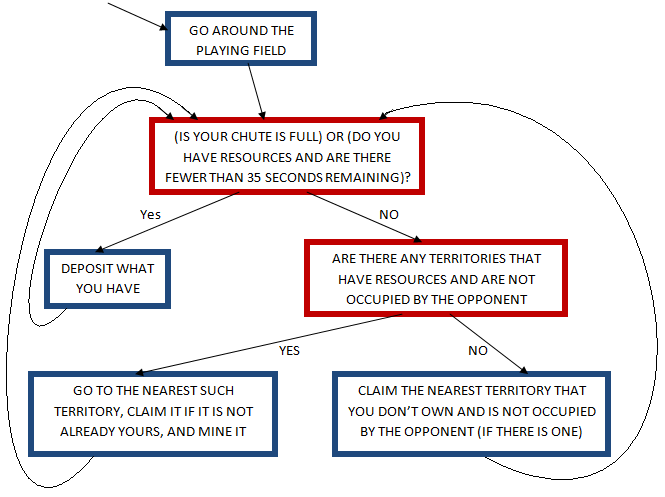
Navigation
Being able to maneuver the playing field quickly and efficiently was another important part of this competition. The standard way to drive from point to point with a non-holonomic robot like Squeaky is to combine two controllers, one for forward velocity and another for rotational velocity. The forward velocity controller outputs a velocity that is proportional to the distance between the current location and the goal point while the rotational velocity controller outputs a velocity that is proportional to the angular error of the heading.
Combining these controllers yields a system that converges to the desired point by tracing a curve that is the solution to some system of linear differential equations. We added two optimizations to this controller, the first was allowing the robot to go backwards if its heading error exceeded π/2. The second optimization was multiplying the forward velocity by some power of the cosine of the angular error. This kept Squeaky from going wide whenever its angular error was large or from orbiting the goal if it happend to be at an unfortunate distance and angle.
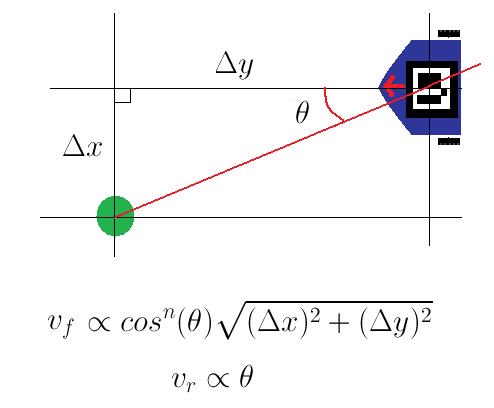
This controller works perfectly when there is a straight-line path between the start and goal. However, this year’s playing field had a large hexagonal hole in the center. This meant that we would have to make some modifications to this controller before we could use it. The first thing we tried was generating a waypoint whenever we wanted to get to a point that is occluded. This approach did not do well in testing. The paths it produced came unsettlingly close to the walls (and occasionally resulted in collisions). Furthermore, the fact that the path had waypoints meant that the robot would waste time converging to points that were not the goal.
It was apparent that we needed something more complicated. We decided that instead of looking for straight-line paths between points, we should try to find paths that curve around the origin. The way to do this is by applying our straight-line controller in a new coordinate system where curves around the origin map to straight lines. We chose polar coordinates, because a linear function between r and θ becomes an Archimedean spiral between x and y. The following picture shows the resulting controller.
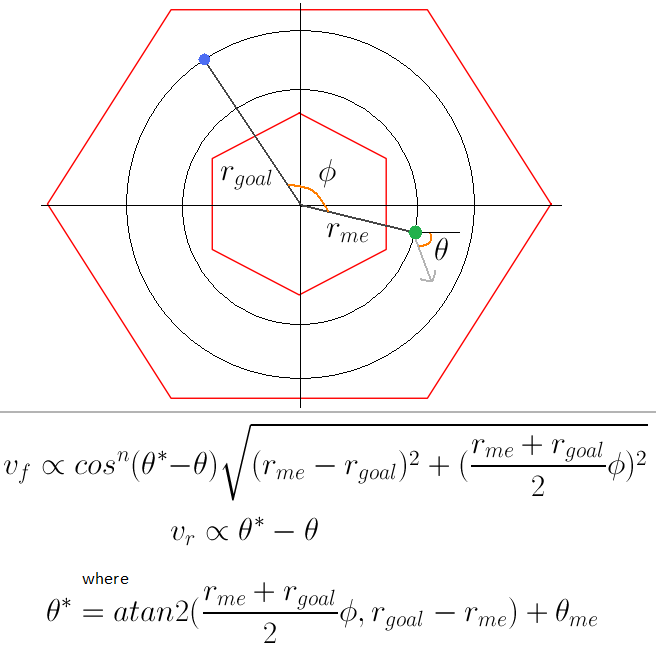
This new controller worked very well. It produced elegant trajectories that that stayed clear of the boundaries. A spiral connecting two points in the playing field does not leave the free space unless one of the points is already along the boundary. This means we have to do no extra work to prevent collisions with the wall. Here is a plot with three simulated paths all going from (24",-10") to (28",28") and with a initial headings of 0, π/3, and 3π/4.
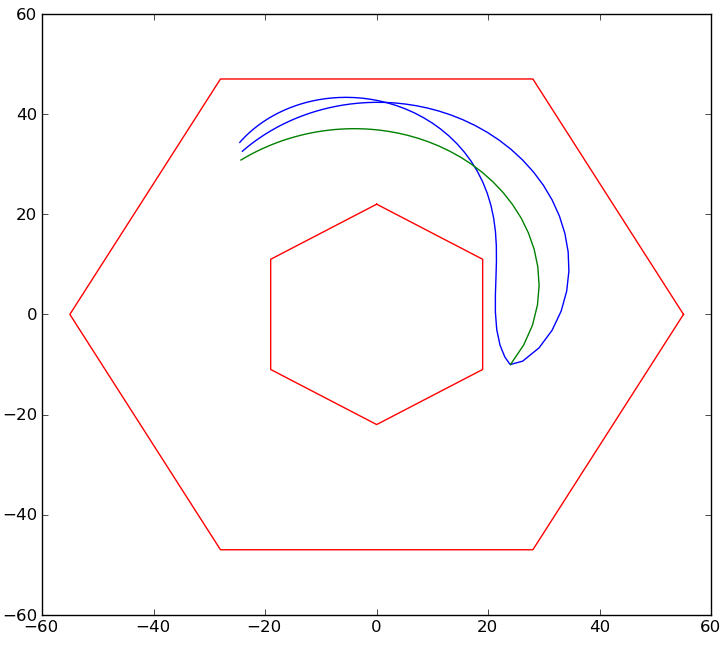
Dealing With Failure
We made several design decisions to minimize the risk of failure and deal with it when it happens. Our main strategy for preventing failure revolved around keeping the code simple. We ran everything on a single thread to prevent any concurrency issues. This limited the amount we could do but it was worth the headaches it spared us. Another design decision we made to prevent failure was to make the motions redundant. Whenever Squeaky approaches a lever or a gearbox, it goes through a three step alignment. First, it goes to a point 12 inches in front of the target. Then, it turns to face the object. Finally, it drives to it. This way we ensure that Squeaky is always facing the right direction when approaching the target.
The worst thing that could happen is for the robot to get stuck in some bad state. This could happen when a function never returns or some loop never terminates. To prevent this, we placed a timeout in every while loop that would cause it to terminate if it went on for longer than some specified amount of time. We added checks to see if functions are returning normally or if they are returning because they timed out and reacted to abnormal returns appropriately.
Because of the limited amount of time and computation power we had, we could not implement any diagnosis and repair mechanisms. This was unfortunate because one of the reasons why we lost our final game was due to the fact that the motor driving the right wheel was getting weaker over time, causing the robot to tend to the right when moving. The robot went wide while in the exploration phase and crashed into a gearbox, losing precious time and exploration points. Dynamically testing and adjusting the relative gains on the motors could have prevented this.